Rivest Shamir Adleman (RSA)
RSA

Rivest Shamir Adleman (RSA) adalah sebuah jenis algoritma asymmetric encryption yang diambil dari nama penciptanya Ron Rivest, Adi Shamir dan Leonard Adleman pada tahun 1977 dengan menggunakan konsep faktorisasi bilangan bulat besar.
RSA menerapkan konsep private key dan public key. Private key digunakan untuk dekripsi data yang telah dienkripsi dengan kunci publik yang sesuai sedangkan Kunci publik digunakan untuk enkripsi data. Kunci publik dapat dengan aman dibagikan kepada siapa pun tanpa membahayakan keamanan data, sementara kunci privat harus tetap dirahasiakan oleh pemiliknya.
Prinsip utama dibalik keamanan RSA adalah kesulitan dalam memfaktorkan bilangan semi prima yang sangat besar menjadi faktor prima. Algoritma ini bergantung pada kesulitan faktorisasi ini untuk menjaga kerahasiaan kunci privat. Dalam implementasi praktisnya, panjang kunci RSA diukur dalam bit, dan semakin panjang kunci, semakin sulit untuk memecahkannya. Masih belum terbayang? Mari bahas lebih detail.
RSA memiliki berbagai aplikasi, termasuk enkripsi komunikasi data, tanda tangan digital, autentikasi pengguna, dan keamanan data secara umum.
Glosarium:
Faktorisasi adalah suatu proses menguraikan bilangan matematika menjadi faktor-faktor yang memperoleh hasil perkalian yang sesuai. Kalau faktor-faktor itu dikalikan dan menghasilkan hasil sesuai dengan faktorisasi maka bilangan-bilangan tersebut merupakan hasil faktorisasi, sebagai contoh 12 faktornya 1, 12, 2, 6, 3, 4.
Bilangan prima adalah suatu bilangan yang lebih besar dari satu dan hanya memiliki 2 faktor yang positif yaitu 1 dan dirinya sendiri. Artinya bilangan ini tidak boleh habis dibagi bilangan lainnya. Contoh bilangan prima 2,3,5,7,13,17, 29.
Bilangan semi-prima adalah suatu bilangan yang faktor-faktornya adalah 2 buah bilangan prima, dan faktor-faktor-nya ini tidak dapat dipecahkan lagi. Atau gampangnya perkalian 2 buah bilangan prima menghasilkan bilangan semi-prima.
Sebagai contoh 6 → 2 x 3
15 → 3 x 5
35 → 5 x 7
Modulus, adalah sebuah operasi yang hasil merupakan sisa pembagian 2 bilangan. Ditandai dengan tanda ‘mod’ atau ‘%’
Sebagai contoh 12%5 = 2, karena maksimal pembagian 12 menggunakan 5 adalah 10 sehingga menyisakan 2, 2 itu adalah yang disebut modulus.
20%5 = 0, artinya 20 habis dibagi 5 artinya 5 adalah faktor dari 20.
Totient merujuk pada fungsi totient Euler pada matematika yang dinotasikan dengan φ(n) atau phi(n), yang merupakan jumlah bilangan bulat positif yang lebih kecil dari n dan relatif prima dengan n. dalam menentukan totient dari bilangan semi-prima adalah dengan mengalikan kedua bilangan prima yang sudah dikurangi 1.
Dalam RSA, proses membuat key sebagai berikut:
-Pilih 2 bilangan prima, misal 7 dan 19 anggap itu sebagai a dan b.
-kalikan keduanya a*b →7∗19=133→semi-prime (anggap sebagai N).
-kalkulasi totient → (a-1)∗(b-1)=6∗18=108 anggap sebagai t.
| a | 7 |
| b | 19 |
| N | 133 |
| t | 108 |
Angka dalam membuat public key ada syarat yang harus dipenuhi: (29) →anggap sebagai c
| -harus bilangan prima | (3) | 5 | 29 |
| -harus lebih kecil dari totient | (3 < 108) | 5 < 108 | 29 < 108 |
| -harus bukan merupakan faktor dari totient | (108%3=0) tidak memenuhi | 108%5 = 3 | 108%29 = 21 |
Angka untuk private key harus memenuhi syarat (41) anggap sebagai e
| Hasil dari perkalian private key dan public key | 41*29 = 1189 | |
| Lalu dibagi dengan totient | 1189 mod 108 = 1 | |
| Sisanya harus 1 | 1 |
Dalam notasi matematika bisa dibuat seperti ini (D∗E) Mod T=1
| a | 7 |
| b | 19 |
| n | 133 |
| t | 108 |
| c | 29 |
| e | 41 |
| Message | 60 |
| message | 65 |
Kita sudah punya angka encryption, pakai itu terhadap algoritma encryption RSA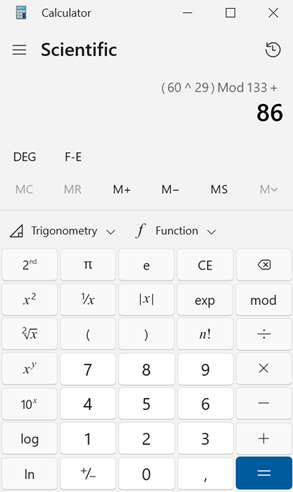 |
Kita sudah punya angka decryption, pakai itu terhadap algoritma decryption RSA
|
| (60^29) mod 133 = 86 | (86^41) mod 133 = 60 |
Dengan begitu hasil dari message dan cipher pasti akan sama
Seberapa amankah RSA ini?
Meskipun kita tau kalau RSA ini dibuat tahun 1977 atau sudah berusia kurang lebih 46 tahun, RSA masih dapat diandalkan untuk melakukan encryption dan decryption dimasa sekarang karena berdasarkan Challenge yang diberikan oleh RSA laboratory, terdapat 54 bilangan semi prima yang dibuat pada 1991 dan barang siapa yang berhasil memecahkan faktorisasi bilangan prima dari bilangan semi-prima tersebut akan mendapatkan imbalan uang. Challenge tersebut berakhir pada 2007 dan dari 54 soal bilangan semi-prima, yang hanya berhasil memecahkan menjadi bilangan prima cuma 12 soal. Terhitung per februari 2020, bertambah menjadi 23 soal yang berhasil dipecahkan. Dan faktorisasi tertingginya adalah 829 bits. Sedangkan standard RSA sekarang adalah 1024 bit, mungkin belum terbayang seberapa banyak, contoh soal diatas menggunakan bilangan semi prima 133 dengan kata lain kalau di konversi menjadi bit (bilangan biner) menjadi 8 bit
- Kalau belum kebayang seberapa besar 1048 bit itu seberapa besar, ini adalah 1048 bit.
| 00010010101101110101010000000010010011010111100000011100000100100011111001101010110000
10100111101101101010010100001100101000111001111001001010110011100111001010011010011100 11101100110110101101011001001100110011001011011111000111001101011111010010110111000110 01011011101110111110111101011000100000010101111001100111111010100110100000100000010011 00001101100101001111001010100101100111010011000001100100011111100000010010011001000110 00001001101010100100110010010000010010010000011110001110000110110100111000001000000011 01001011101100110110000010000010010011100111001000010110001010000101010101101100000000 01110001000101000111000110111001110011111101100001000000101110000101011100101010110000 01001011101110100001000000000010111011100001010100101001001001111010011110111100100001 00010000000000010110100000111011100100001100010101100111101001101101100001101011100010 11100101100110011101000000000011001111100000111110101110010000100000000111001011110101 101001110110011100111101011011001110010011010111100010100111001011001011011011 |
Dan inti dari RSA menjadi aman itu karena kesulitan dalam memfaktorkan bilangan semi prima yang sangat besar menjadi faktor prima-nya, kalau sudah menemukan faktor prima maka kita dapat dengan gampang membuat public dan private key.