Introduction to Binary Code

27 Nov 2022

Articles

Latar Belakang Kode Biner

Semua bahasa pemrograman memiliki pondasi yang berdasarkan pada kode biner. Bisa dikatakan ini adalah bagian belakang dari semua fungsi komputer. Kode biner terdiri dari serangkaian angka 0 atau 1, meskipun hanya terdapat dua karakter angka yang dipakai kode biner masih dapat diartikan dalam berbagai variasi sistem komputer. Semua fungsi komputer akan dengan cepat beralih antara 00 atau 01 pada kecepatan yang tidak dapat dipahami. Beginilah cara komputer membantu manusia dalam menyelesaikan tugas-tugas yang akan memakan waktu lebih lama untuk diselesaikan. Otak manusia berfungsi secara holistik pada kecepatan yang jauh lebih cepat daripada komputer dalam melakukan jenis tugas yang sangat rumit lainnya, seperti proses berpikir dan proses analisa suatu hal. Kode dalam bahasa komputer akan dibaca oleh unit pemrosesan pusat atau CPU dari komputer berdasarkan pada string ASCII yang distandarisasi dengan string nol yang mewakili setiap huruf dari alfabet atau angka.

Sebelum itu, kita juga perlu mengerti definisi dari ASCII. ASCII adalah singkatan dari American Standard Code Information Interchange, yang dapat didefinisikan berupa standar kode biner 7 bit yang akan diterjemahkan ke dalam logika komputer untuk mewakili teks, huruf, dan simbol yang dikenali manusia. Terdapat 0 sampai dengan 127 angka atau huruf yang diwakili dalam sistem ASCII. Setiap string biner memiliki delapan bit biner yang akan terlihat seperti sekelompok nol dan yang dalam pola unik tertentu merepresentasikan setiap huruf dalam kata. Dengan jenis kode ini, 256 nilai yang berbeda dapat mewakili suatu kelompok besar simbol, huruf, dan instruksi pengoperasian yang dapat diberikan ke mainframe. Dari kode-kode ini, diturunkan string karakter dan string bit yang mewakili angka desimal. Angka-angka biner dapat ditemukan dalam literatur Vedic, Shastras, yang ditulis dalam bahasa pertama umat manusia yaitu, bahasa Sansekerta, khususnya yang terletak di Chanda Sutra yang pertama kali ditulis dalam bentuk teks oleh Pingala sekitar abad ke-4. Ini adalah perkiraan, karena bahasa Sanskerta adalah bahasa yang telah dinyanyikan bertahun-tahun sebelum umat manusia beralih menulis di atas kertas. Sebelum kebutuhan untuk menulis di atas kertas, umat manusia memiliki ingatan yang sangat tinggi sehingga kebutuhan untuk menulis bahkan tidak menjadi bagian dari kebudayaan pada waktu itu.

Dalam dokumen sejarah yang lebih modern, dicatat bahwa perkembangan umat manusia telah jauh melampaui bahasa Sanskerta. Saat itu, tidak ada teks tertulis karena informasi-informasi penting dibacakan secara lisan. Tidak ada buku teks sebelum pembuatan kode biner, karena hal ini dianggap tidak diperlukan. Menurut Shastras, umat manusia menjadi kurang beruntung dan ingatan mereka mulai menurun sehingga mereka membutuhkan teks dan buku yang harus dibuat untuk melacak informasi penting. Kemudian, hal ini menjadi suatu keharusan. Kode biner pertama kali ditelusuri dari teks-teks tersebut.

Setelah selang waktu yang cukup lama, sekitar abad ke-17, seorang filsuf besar yang juga merupakan bapak Kalkulus, Gottfried Leibniz memperoleh sistem logika dari pernyataan verbal yang sepenuhnya direpresentasikan ke dalam kode matematika. Dia berteori bahwa kehidupan dapat direduksi menjadi suatu kode-kode sederhana, seperti deretan kombinasi 0 dan 1. Meskipun tidak benar-benar mengetahui apa yang akan digunakan sistem ini, pada akhirnya, dengan bantuan George Boole, logika Boolean dikembangkan menggunakan sistem on / off dari 0 dan 1 untuk operasi dasar pada aljabar. Kode hidup atau mati dapat dengan cepat diterapkan oleh komputer untuk melakukan aplikasi yang jumlahnya tampaknya tidak terbatas. Semua bahasa komputer didasarkan pada sistem logika biner.

Jenis Kode Biner Yang Digunakan Dalam Aplikasi Modern

Konsep di balik sistem biner mungkin tampak seperti sesuatu yang digunakan oleh komputer generasi sebelumnya, tetapi sistem ini masih dianggap sebagai bagian penting dalam dunia teknologi modern saat ini. Ini adalah bahasa komputer dalam bentuknya yang paling mentah, karena komputer dan peralatan elektronik lainnya yang dijalankan oleh sirkuit digital berkomunikasi menggunakan dua konsep yang sama: 0 dan 1 atau hidup dan mati. Apakah itu menyimpan data, menjalankan perintah, atau aplikasi lain apa pun, komputer dan sistem digital lain yang tersedia saat ini menggunakan berbagai jenis kode biner untuk melakukan tindakan yang diinstruksikan pengguna melalui antarmuka pengguna grafis. Agar kita dapat memahami dan berkomunikasi dengan komputer, konversi harus dilakukan dari kode biner menjadi bentuk yang lebih dimengerti manusia. Salah satu cara paling sederhana untuk mengubah biner menjadi bentuk yang dimengerti, seperti teks, desimal, heksadesimal, oktal, atau sistem lain, adalah dengan menggunakan konverter biner.

Untuk mendapatkan pemahaman yang mendalam tentang kode biner dan aplikasinya di dunia modern, ada baiknya kita mengetahui berbagai jenis kode biner yang digunakan dalam aplikasi modern. Kode biner diklasifikasikan ke dalam beberapa kategori antara lain weighted code, binary coded decimal (BCD) code, non-weighted code, alphanumeric code, dan error code.

Weighted Code

Kode biner ini mengikuti prinsip posisi di mana setiap digit dalam angka diberi nilai atau bobot tertentu sebelum dikonversi, dan nilai itu juga tergantung pada posisi bit biner. Ada beberapa sistem kode yang digunakan untuk menunjukkan atau mendefinisikan angka desimal antara 0 dan 9. Dalam sistem weighted code, masing-masing digit desimal dalam angka diwakili oleh sebuah set empat bit. Beberapa penggunaan weighted code antara lain merepresentasikan angka desimal pada volt meter, kalkulator, dan perangkat elektronik lainnya, menampilkan fungsionalitas input / output pada sirkuit digital, dan memanipulasi data pada berbagai jenis operasi aritmatika.

Binary Coded Decimal (BCD) code.

Salah satu jenis kode yang paling populer adalah kode BCD yang digunakan dalam berbagai aplikasi modern. Jenis kode ini terdiri dari angka desimal di mana angka biner 4-bit mewakili setiap digit. Ini adalah cara yang hebat dan lebih halus mendefinisikan angka desimal dengan bantuan kode biner karena metode ini memungkinkan pengguna untuk mewakili enam belas angka, mulai dari 0000 hingga 1111. Namun, hanya sepuluh digit pertama yang digunakan dalam BCD, sementara enam kode kombinasi yang tersisa dianggap tidak valid. Ada beberapa keuntungan dari kode BCD, yang utama adalah bahwa kode ini sangat mirip dengan sistem desimal, memungkinkan pengguna untuk hanya mengingat konversi angka desimal dari 0 menjadi 9. Dan dengan begitu banyak konverter biner online, tugas ini dapat sangat mudah . Namun, karena metode ini sedikit berbeda dari yang lain, Anda mungkin akan menghadapi beberapa kesulitan. Misalnya, aritmatika BCD dianggap lebih kompleks. Demikian pula, aturan penambahan dan pengurangan agak berbeda dalam BCD. Selain itu, BCD membutuhkan lebih banyak bit daripada kode biner utama untuk mewakili angka desimal. Dengan kata lain, dapat dikatakan bahwa itu sedikit tidak efisien daripada biner.

Non-Weighted Code

Jenis kode biner ini tidak melibatkan penetapan bobot posisional, tetapi masih melakukan konversi dari biner ke sistem lain. Non-weighted code ini dapat digunakan untuk deteksi kesalahan dalam operasi yang berbeda, untuk mengubah posisi, dan untuk melakukan jenis operasi aritmatika tertentu. Contoh dari non-weighted code adalah gray code, excess-3 code, dan non-weighted BCD code.

Gray Code

Gray code adalah jenis lain dari non-weighted code yang tidak terhubung dengan kode aritmatika yang artinya ia tidak memiliki bobot khusus yang dialokasikan untuk posisi bit tertentu. Dengan kata lain, ini adalah cyclic code. Dalam metode ini, hanya satu bit dari angka biner yang diubah ketika angka desimal dipindahkan ke yang berikutnya. Karena hanya satu bit yang diubah, gray coding method juga dikenal sebagai unit distance code. Beberapa aplikasi gray coding method termasuk encoders posisi poros yang menghasilkan kata kode yang mewakili posisi sudut poros.

Excess-3 Code

Juga dikenal sebagai kode XS-3, ini adalah metode non-weighted code yang umum digunakan untuk mendefinisikan angka desimal. Pada code ini, ada kode 4-bit yang penting, kemudian bentuk kode BCD digunakan dengan nomor BCD. Kode ini sebelumnya digunakan dalam menambahkan mesin dan komputer lama. Kode ini berasal dari kata 8421 BCD yang ditambahkan ke (3) 10 atau (0011)2 dari setiap kata kode dalam BCD tertentu. Penggunaan kode XS-3 yang paling umum adalah operasi pengurangan dalam sistem digital. Bagian terbaiknya adalah kode ini merupakan kode yang dapat melengkapi dirinya sendiri, yang berarti bahwa 1 komplemen akan menghasilkan 9 angka pelengkap dari angka yang dikodekan.

Alphanumeric Code

Ini adalah fakta mapan bahwa representasi bit atau digit biner terbatas hanya pada dua simbol, yaitu 0 dan 1. Namun, karena komputer telah berevolusi secara signifikan selama beberapa tahun terakhir, ini telah membuat komunikasi antara dua komputer menjadi sulit karena ada banyak simbol yang termasuk dalam komunikasi. Misalnya, ada 26 huruf dengan variasi kecil dan huruf besar, tanda baca, angka dari 0 hingga 9, karakter khusus, dan banyak simbol lainnya. Dalam situasi seperti itu, kode alfanumerik yang digunakan memiliki kemampuan untuk mewakili huruf dan angka. Tidak hanya itu, mereka juga dapat digunakan untuk mewakili karakter, seperti simbol dan beberapa bentuk instruksi yang diperlukan untuk mentransfer informasi dari satu perangkat ke perangkat lainnya. Kode alfanumerik dapat mewakili total 36 item, yaitu 26 huruf dan 10 digit. Beberapa kode alfanumerik yang paling umum digunakan untuk representasi data adalah kode EBCDIC dan kode ASCII. Pertama, Extended Binary Coded Decimal Interchange Code (EBCDIC) merupakan kode alfanumerik 8-bit yang dikembangkan oleh IBM, yang mampu mendukung 256 simbol, yang digunakan untuk mengoperasikan komputer mainframe IBM. Kedua, American Standard Code for Information Interchange (ASCII) merupakan kode yang lebih populer di seluruh dunia daripada EBCDIC. ASCII adalah kode alfanumerik untuk 7-bit dan 8-bit. Kode 7-bit mendukung 127 karakter sedangkan kode 8-bit mendukung 256 karakter.

Error Code

Beberapa teknik kode biner digunakan untuk mendeteksi dan memperbaiki kesalahan dalam data yang biasanya terjadi selama transmisi data. Kode-kode ini adalah bit tambahan data, yang dikenal sebagai bit paritas (parity bit) yang digunakan pada saat pengiriman pesan dan yang memungkinkan pengguna untuk menentukan adanya segala jenis kesalahan. Bit paritas yang ditambah dengan bit data akan bersama-sama membentuk suatu kata kode. Ada dua penggunaan error code, yaitu untuk mendeteksi dan untuk mengkoreksi. Pada kegunaan pertama, error code digunakan untuk deteksi. Selama pengiriman pesan, ada kemungkinan bahwa pesan tersebut teracak oleh noise yang mengakibatkan data rusak. Untuk mencegah hal ini terjadi, kode pendeteksi kesalahan dirancang berupa paket data tambahan yang dilampirkan bersama dengan pesan digital. Ini akan membantu dalam mendeteksi apakah pengiriman pesan terputus atau rusak karena kesalahan. Salah satu metode umum dari error-detection code adalah pemeriksaan paritas (parity check). Pada penggunaan kedua, error code digunakan untuk koreksi. Untuk melancarkan proses, kode koreksi kesalahan (error-correcting code) digunakan bersama dengan kode pendeteksi kesalahan (error-detection code) untuk mencari tahu pesan asli sebelum rusak. Kode-kode ini digunakan dengan cara yang sama seperti kode kesalahan untuk deteksi. Bagian terbaiknya adalah error-correcting code juga mampu mendeteksi lokasi yang tepat dari bit data yang rusak.

Cara Kerja Bilangan Biner

Seperti yang diketahui diatas, binary code menggunakan sistem bilangan biner atau bilangan basis 2 yang terdiri dari bilangan 0 dan 1. Sistem biner merupakan bahasa utama dari sebuah sistem komputasi. Di dalam sistem ini, bilangan biner terdiri dari serangkaian delapan bit. Serangkaian delapan bit tersebut merupakan sebuah byte. Dalam skema biner, posisi setiap digit menentukan nilai desimalnya. Jadi, dengan memahami posisi setiap bit, bilangan biner dapat diubah menjadi bilangan desimal.

Dalam bilangan biner penghitungan angka dimulai dari kanan ke kiri. Bilangan bit paling kanan akan dimulai dari 20 dan pangkatnya akan bertambah setiap bilangan bit sebelah kirinya seperti pada tabel dibawah ini

Contoh: 10101100

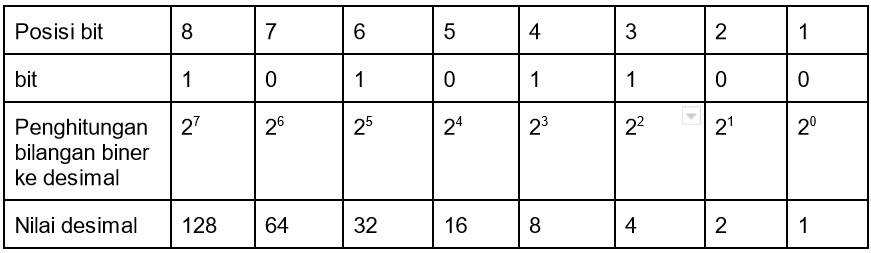
Nilai akhir dari desimal adalah dengan menjumlahkan nilai dari desimal bilangan bit yang bernilai 1. Maka contoh diatas akan bernilai 128+32+8+4 = 172.

Jadi nilai desimal dari 10101100 = 172

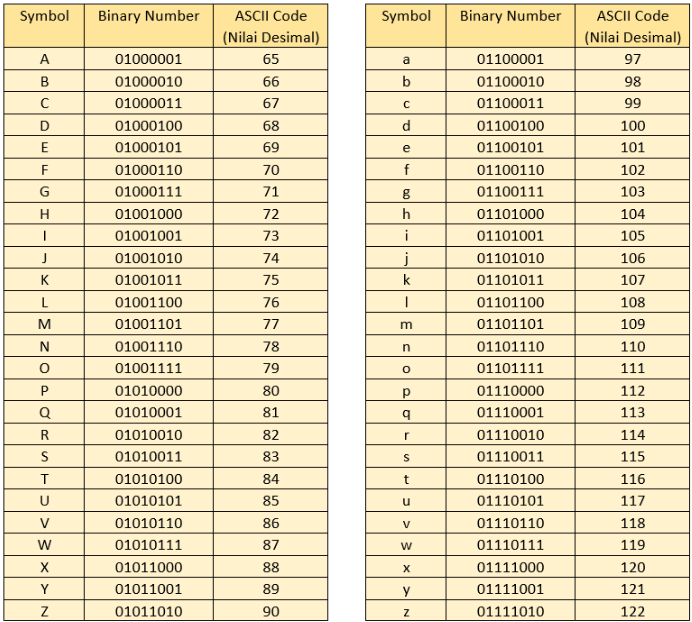
Dari cara kerja atau penghitungan bilangan biner tersebut, maka diterapkan dalam ASCII Code untuk merubah bilangan-bilangan biner tersebut menjadi sebuah karakter. Berikut ini tabel ASCII Code untuk huruf besar dan huruf kecil.

Referensi:

Daniel Eduardo Daud & Pitra Winarianto