Angka Imajiner
Pernahkah saat kalian mengerjakan soal aljabar lalu menemukan soal seperti ini “x2 -1 =0”? biasanya kita akan mencari angka “x” dengan memindahkan angka 1 ke kanan dan melakukan pengakaran di kedua sisi seperti ini “√x2 = √1” dengan begitu kita mendapatkan hasil dari x yakni 1. Namun bagaimana jika soal yang keluar seperti ini “x2 + 1 =0”? kita pasti menggunakan cara yang sama seperti soal sebelumnya dan mendapatkan hasil seperti ini “√x2 = √-1”. √x2 adalah x. Namun, apa hasil dari √-1? Saat kita menghitungnya, kita akan sadar bahwa tidak ada hasil yang dapat kita temukan jika menggunakan bilangan rill. Jadi apa jawaban dari √-1? Disinilah angka imajiner dengan simbol ἰ muncul, sehingga jawaban dari √-1 adalah ἰ. Karena ἰ adalah hasil dari √-1, maka bisa dipastikan bahwa ἰ2 adalah √-1 * √-1 yang mana hasilnya adalah -1.
Angka imajiner muncul di dunia ini untuk menyelesaikan segala permasalahan matematika yang tidak memiliki hasil bilangan rill. Angka imajiner ditemukan oleh matematikawan Yunani yang dipanggil Hero of Alexandria, yang kemudian dikembangkan oleh matematikawan lain seperti Rafael Bombelli, Gerolamo Cardano, dan lain-lain.
Contoh soal
akar
√-4 = 2ἰ
√-18 = ἰ√9 * √2 = 3ἰ √2
Perkalian
Dalam perkalian, gunakan aturan eksponen ax * ay = ax+y
2ἰ * 3ἰ = 6ἰ2
3ἰ2 × -5ἰ3 = -15ἰ5 = -15(ἰ 2)2 ἰ = -15 (-1)2 i = -15
Pembagian
Dalam melakukan pembagian, gunakan aturan eksponen ax / ay = ax-y
4ἰ/2ἰ = 2
6ἰ3 / 7ἰ6 = 6/7ἰ3 = -6/7ἰ = 6ἰ/7
Angka imajiner merupakan angka yang termasuk dalam bilangan kompleks, dalam hal dasar angka imajiner biasanya akan muncul jika kita mengerjakan berbagai macam soal yang menggabungkan pengakaran dan angka minus seperti yang sudah dijelaskan di atas. Angka imajiner digunakan di berbagai bidang seperti di mekanika kuantum dan listrik.
Dalam geometri, penggunaan angka imajiner digunakan sebagai titik-titik yang menandakan sumbu vertikal. Hal ini ditunjukan dari bilangan kompleks yang memiliki rumus a+bἰ, salah satu contohnya adalah 5+2ἰ yang memiliki arti (5,2) .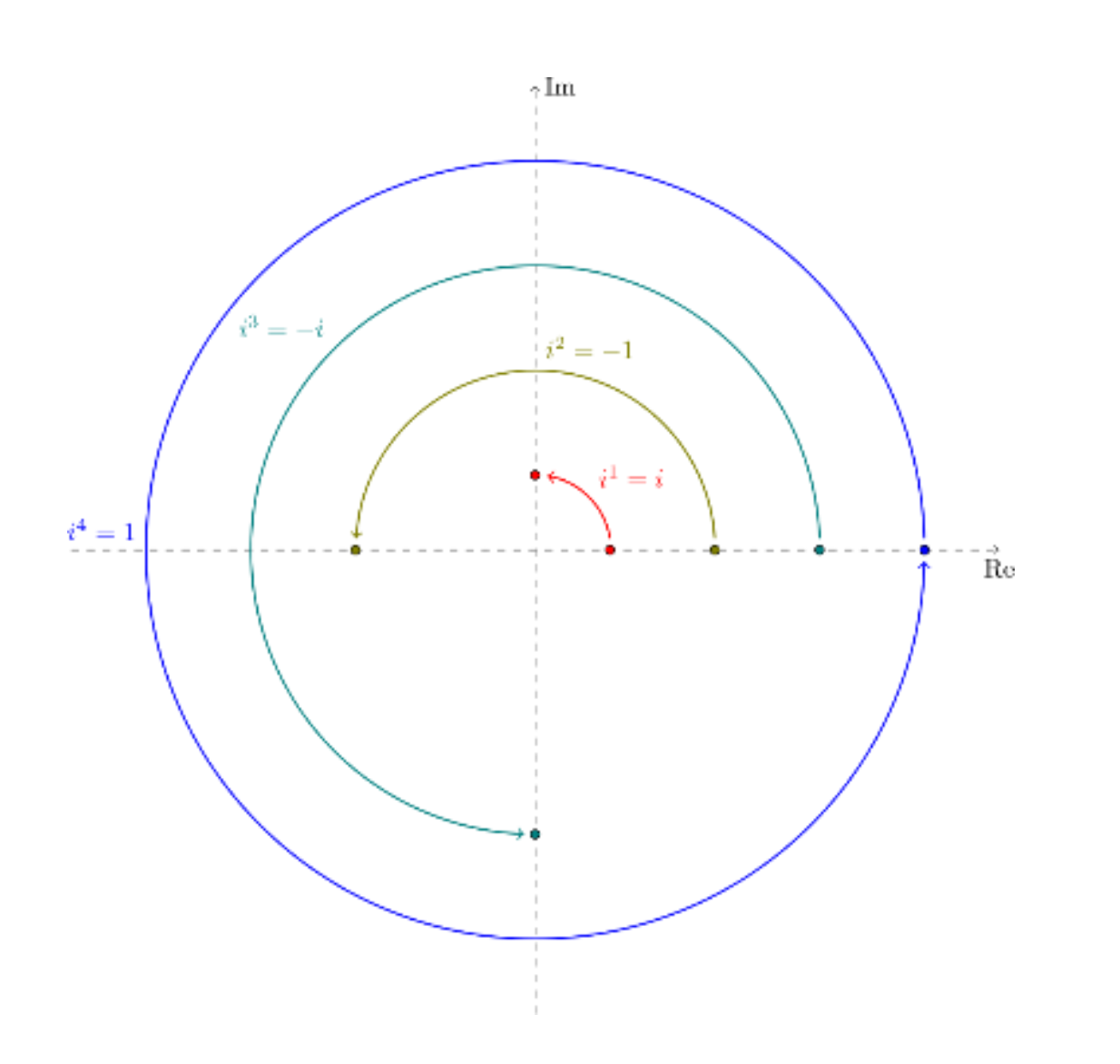
Gambar di atas menandakan bahwa ἰ jika dikalikan dengan ἰ maka akan membuat suatu rotasi 90 derajat berlawanan arah jarum jam dan semakin besar jumlah ἰ yang dilakukan maka rotasi akan semakin banyak berputar.
Referensi:
https://www.cuemath.com/numbers/imaginary-numbers/
https://www.advernesia.com/blog/matematika/bilangan-imajiner/


